7.5. Elastic Deformation

Hooke’s Law states

\[ F = kx \]

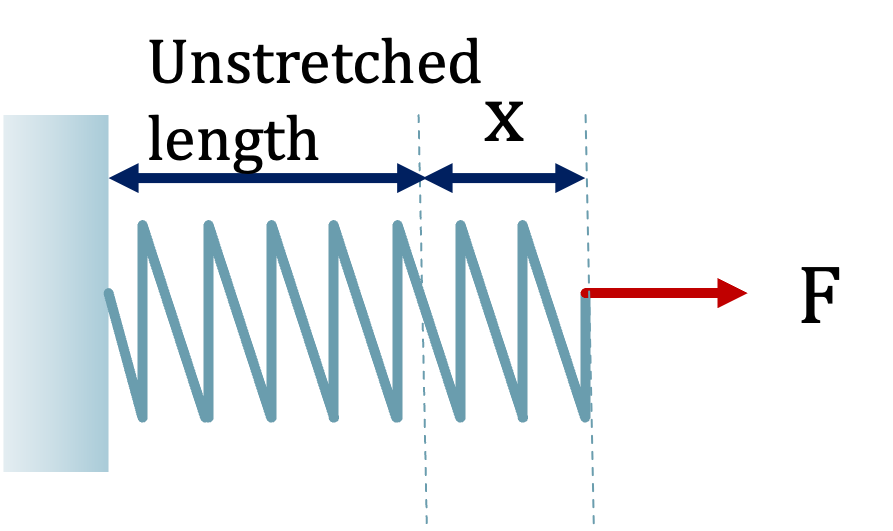
Within the linear-elastic region we can use a similar mathematical form relating stress and strain

\[ \sigma = E\epsilon \]

Where \(E\) is the proportionality constant called the Modulus of Elasticity or Young’s Modulus, which is material dependent.

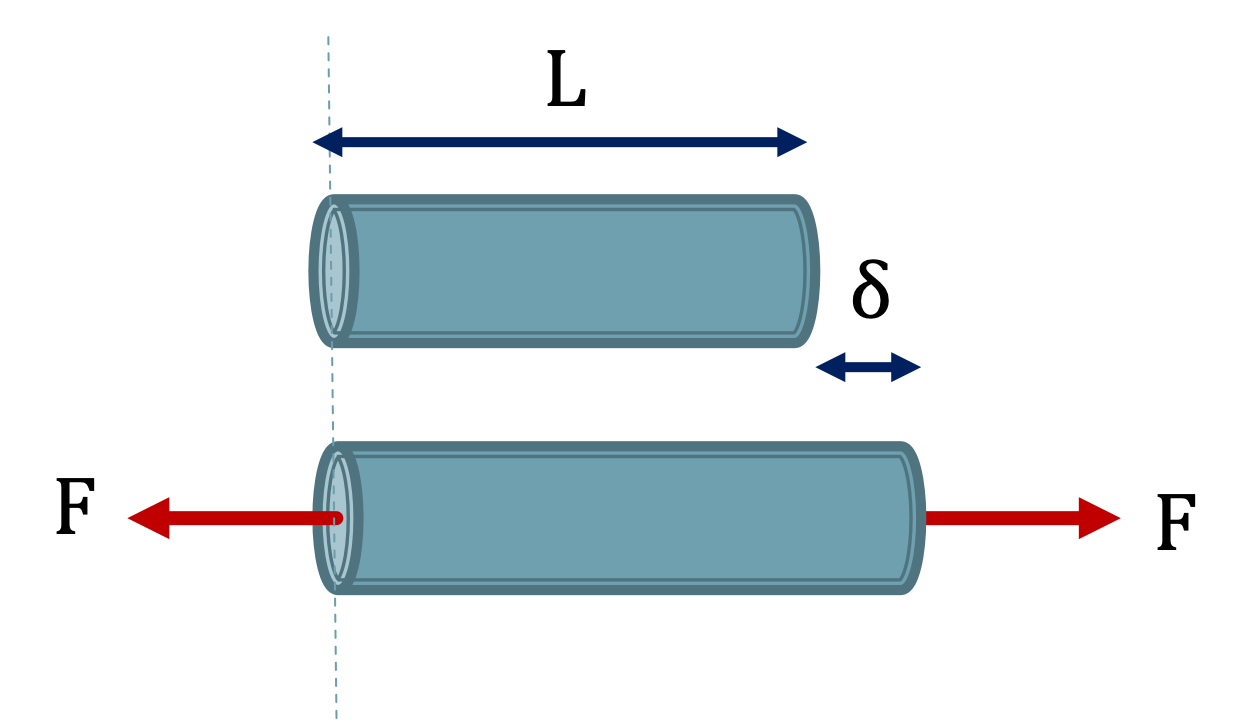
Using this relation we can substitute in the previous definitions for stress and strain

\[ \sigma = E\epsilon \]

\[ \frac{P}{A} = E \frac{\delta}{L} \]

And solve directly for deformation \(\delta\).

\[ \delta = \frac{PL}{AE} \]

Note

Remember, solving for \(\delta\) using the equation above is only valid within the linear elastic region