Ohm’s Law

4.3. Ohm’s Law#

Learning Objectives#

By the end of this section, you will be able to:

  • Describe Ohm’s Law

  • Re-write Ohm’s Law in three ways that solves for voltage, current, and resistance.

  • Recognize how to solve for voltage, current, and resistance.

Ohm’s Law#

Ohm’s Law states that the potential difference across a conductor is directly proportional to the current.

\[ V \propto I \]

Where \(V\) is the potential difference and \(I\) is the current.

Introducing a constant of proportionality \(R\), denoting resistance, Ohm’s law can be writen as:

\[ V = IR \]
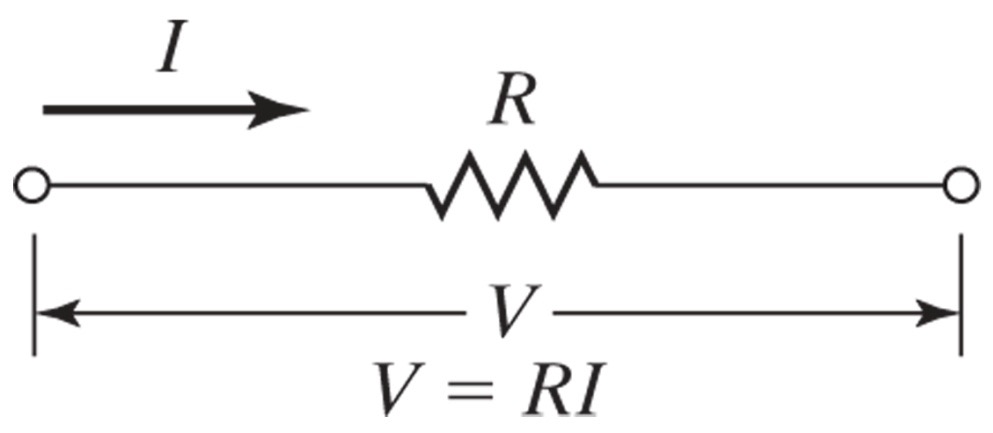
Schematic diagram of a circuit with a resistor labeled "R", current "I", voltage "V", and equation "V=RI"

Resistance#

Electrical resistance, \(R\), is an impedance to current flow through a circuit.

shematic diagram of a resistor symbol

By rearranging Ohm’s law, the resistance between any two points of a conductor is determined by applying a potential difference (\(V\)) between those two points and measuring the current, \(I\), that results.

\[ R = \frac{V}{I} \]

The SI unit for resistance is ohm (\(\Omega\))

\[ 1 \ \Omega = \frac{1 \ V}{1 \ A} \]

Voltage, Current, and Resistance#

Using Ohm’s Law, any one of voltage, current or resistance can be represented in terms of the other two.

A triangle with voltage (\(V\)), current (\(I\)), and resistance (\(R\)) shown below can be helpful to remember these relationships.

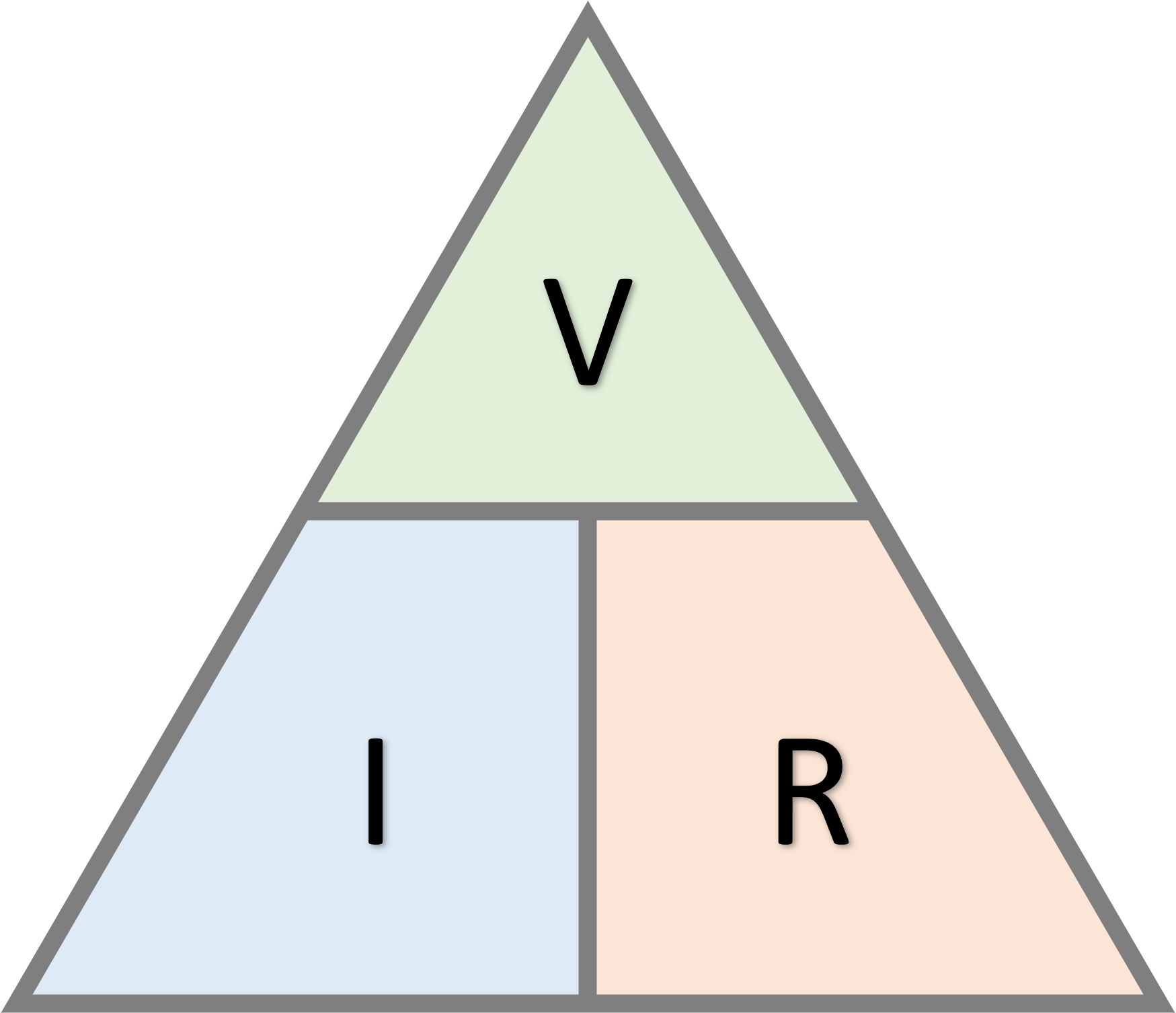
voltage current resistance triangle

\[ V = IR \]
\[ I = \frac{V}{R} \]
\[ R = \frac{V}{I} \]

It is often necessary to find the equivalent or total resistance of two or more resistors connected together. Two ways to connect resistors together is in series or in parallel. Combinations of resistors will be addressed in the next section.

Contents