Power

4.6. Power#

The electric potential difference, or voltage \(V\), between two points is work done in moving a charge from one point to the other.

\[ V = \frac{dw}{dq} \]

By definition the rate at which work is done is power, \(P\).

\[ P = \frac{dw}{dt} \]

Using the definition of instantaneous voltage, and rearranging to solve for the change in work \(dw\):

\[ dw = vdq \]

The change in work, \(dw\) per unit time \(dt\) is therefore:

\[ \frac{dw}{dt} = v \frac{dq}{dt} \]

But remember, the definition of current is \(i=\frac{dq}{dt}\), thus Power can be written as:

\[ P = vi \]

For simpler DC-steady state circuits:

\[ P = VI \]

Units of Power#

Power is equal to voltage times current.

\[ P = VI \]

SI units for voltage \(V\) are \([\frac{J}{C}]\) and the SI units for current \(I\) are \([\frac{C}{s}]\).

\[ P = \left[\frac{J}{C}\right]\left[\frac{C}{s}\right] \]

Canceling the units coulombs, \(C\), power \(P\) ends up in units of \([\frac{J}{S}]\). One joule (\(J\)) per second (\(s\)) is equal to one watt (\(W\)).

\[ P = \left[\frac{J}{s}\right] = [W] \]

Power, Current, Voltage and Resistance#

When current flows through a resistor, the absorbed electrical energy is dissipated as thermal energy.

The rate at which this occurs is referred to as power dissipation.

\[ P = VI \]

Using Ohm’s law, two alternate forms relating power to current, resistance, and voltage can be created using

Ohm’s law as \(V = IR\)

\[ P = I^{2}R \]

Ohm’s law as \(I=\frac{V}{R}\)

\[ P = \frac{V^2}{R} \]

The image below shows how power, voltage, current and resistance can all be related.

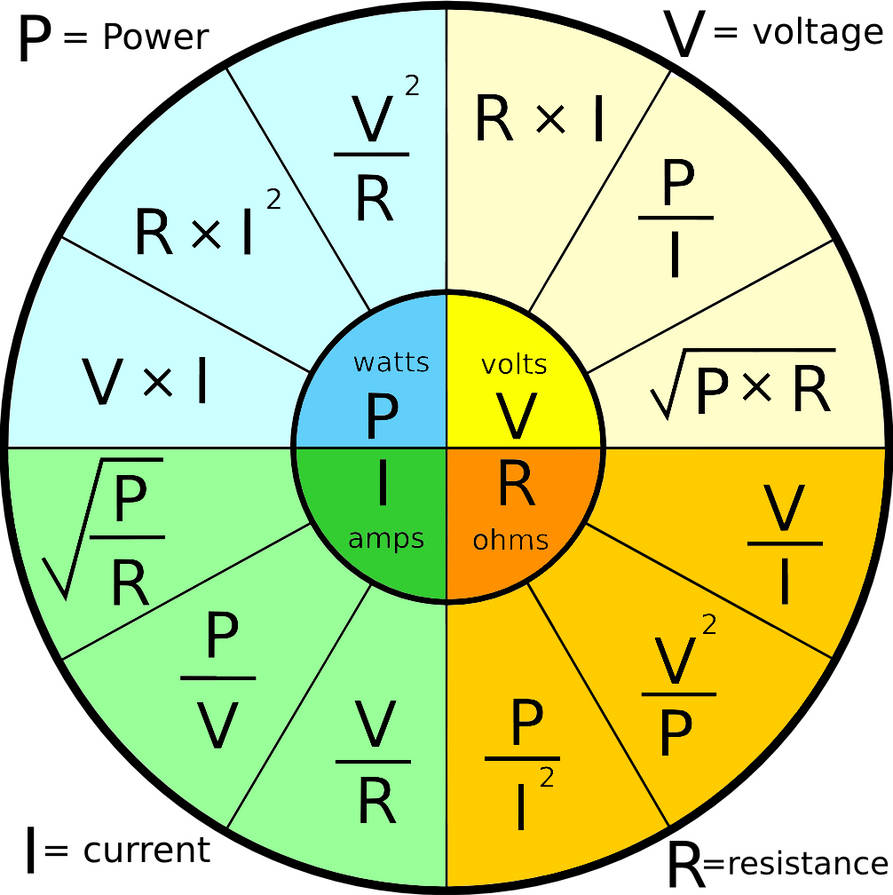power voltage current resistance wheel Image Credit: WireCharm, Creative Commons Attribution 3.0 License

Worked Example

GIVEN:

The circuit diagram below:

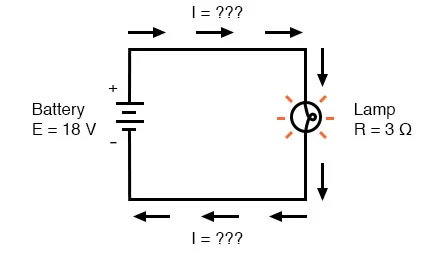
circuit with battery and lamp

Image Credit: Applied Industrial Electricity, Design Science License

In the above circuit, we know we have a battery voltage of 18 volts and a lamp resistance of 3 \(\Omega\).

FIND:

The electrical power disspated by the lap, \(P_l\)

SOLUTION:

In the above circuit, we know we have a battery voltage of 18 volts and a lamp resistance of 3 \(\Omega\). Using Ohm’s Law to determine current, we get:

\[ I = \frac{V}{R} = \frac{18 V}{3 \Omega} = 6 A \]

Now that we know the current, we can take that value and multiply it by the voltage to determine power:

\[ P = VI = (18 V)(6 A) = 108 W \]

This tells us that the lamp is dissipating (releasing) 108 watts of power, most likely in the form of both light and heat.

\[ P_l = 108 W \]
Contents