2.2. Units and Dimensions#
Learning Objectives#
By the end of this section, you will be able to:
Describe how SI base units are defined
Describe how derived units are created from base units
Express quantities given in SI units using metric prefixes
Units and Physical Quantities#
The measurement of physical quantities and the expression of physical principles through mathematical relationships unlocks a deep understanding of the natural world. To effectively convey and manipulate the vast ranges encompassed by these measured and calculated values, we must adopt a universally accepted system of units. All physical quantities can be expressed in terms of seven fundamental base quantities.
Note
A a physical quantity is defined either by how it is measured or by stating how it is calculated from other measurements or calculations. For example, we can define distance and time by measuring them with a meter stick and stop watch. Then we can define average speed by calculating the measured distance divided by the measured time.
Measurements of physical quantities are expressed in terms of units. For example, the length of a race can be expressed in units of meters (for sprinters) or kilometers (for distance runners). Without standardized units, it would be extremely difficult for engineers to express and compare measured values in a meaningful way.
Unit Systems#
There are two major systems of units used worldwide:
SI Units (French Système International d’Unités), also known as the metric system
USCS Units (United States Customary System), also called English or Imperial Units
The USCS unit system was historically used in nations formerly occupied by the British Empire. USCS units are still widely used today in the United States. You may also encounter SAE units, named for the Society of Automotive Engineers. Fasteners (such as nuts and bolts) and automotive tools (such as wrenches and sockets) measured in inches, rather than metric units, are sometimes called SAE fasteners or SAE wrenches.
Virtually every country in the world (except the United States) uses SI units. The metric system is also the standard system agreed on by engineers and scientists.
Base Units#
The International Standards Organization (ISO) defines seven base quantities, which form the International System of Quantities (ISQ). These seven base quantities are used to define seven SI base units. The table below lists the seven base quantities and the corresponding SI base units.
ISQ Base Quantity |
Base Quantity Symbol |
SI Base Unit (abbreviation) |
|---|---|---|
Length |
L |
Meter (m) |
Mass |
m |
Kilogram (kg) |
Time |
t |
Second (s) |
Electric Current |
I |
Ampere (A) |
Temperature |
T |
Kelvin (K) |
Amount of a substance |
n |
Mole (mol) |
Luminous Intensity |
\(I_v\) |
Candela (cd) |
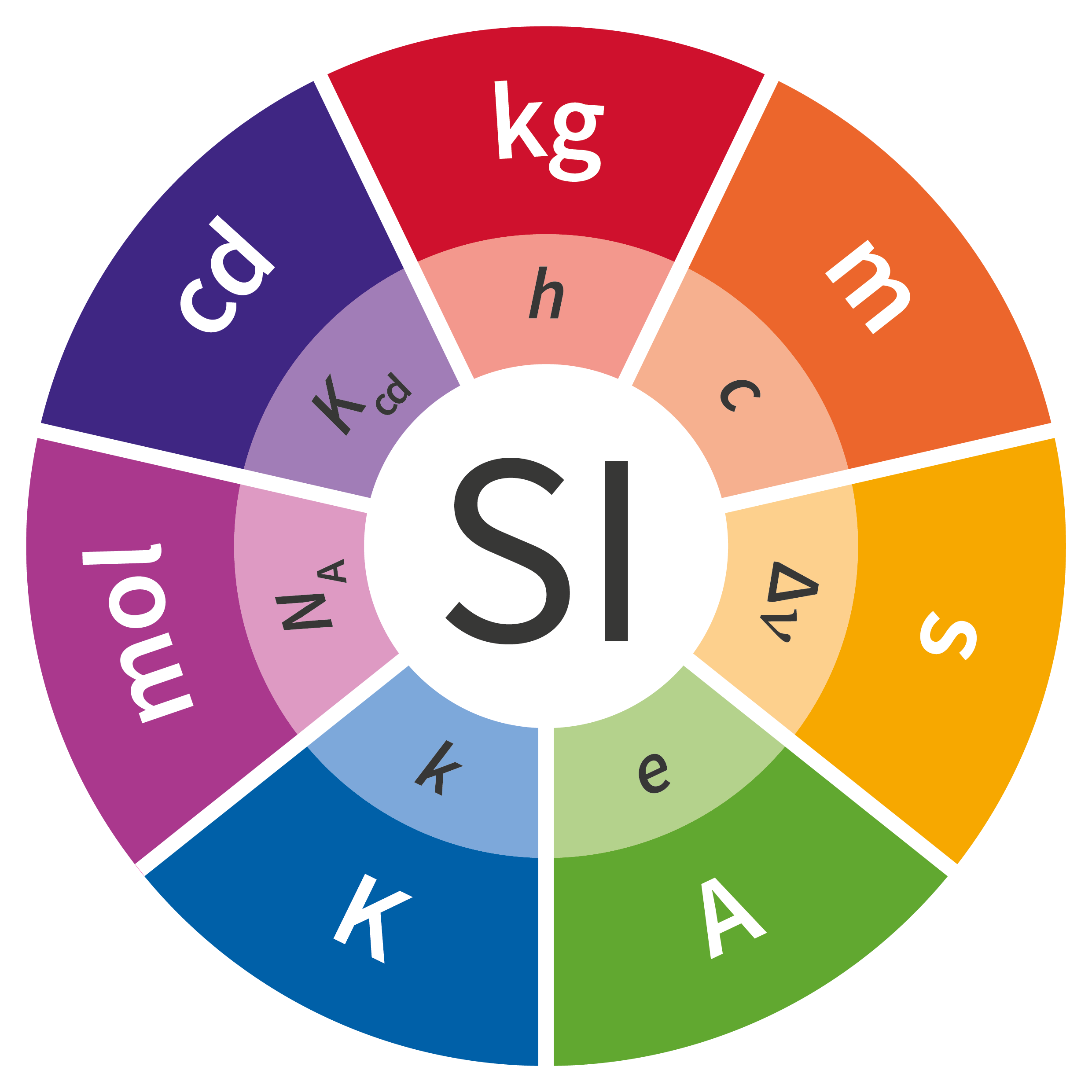
Fig. 2.1 SI Base Quantities#
Worked Example
Question: Which of the following is not a base dimension?
a. Length
b. Mass
c. Weight
d. Time
Answer
Answer: c. Weight
Derived Units#
You are probably familiar with some derived quantities that can be formed from the base quantities listed in the table above. For example, the geometric concept of area is always calculated as the product of two lengths. Therefore, area is a derived quantity that can be expressed in terms of SI base units using square meters (\(m \times m = m^2\)). Similarly, volume is a derived quantity that can be expressed in cubic meters (\(m^3\)). Speed is length per time; so in terms of SI base units, we can measure speed in meters per second (\(m/s\)). Density is mass per volume, which is expressed in terms of SI base units such as kilograms per cubic meter (\(kg/m^3\)).
Depending on your background and interests, you may be able to come up with other derived quantities, such as the mass flow rate (\(kg/s\)) or volume flow rate (\(m^{3}/s\)) of a fluid, electric charge (\(A \cdot s\)), mass flux density \(kg/(m^2 \cdot s)\). Every physical quantity can be derived from the seven base quantities and the units of every physical quantity can be derived from the seven SI base units.
SI Derived Units#
The table below specifies a number of derived units in the SI unit system.
Quantity |
SI Unit |
Unit Name |
Base Units |
|---|---|---|---|
Frequency |
Hz |
hertz |
\(s^{-1}\) |
Force |
N |
newton |
\(kg \ m \ s^{-2}\) |
Pressure |
Pa |
pascal |
\(kg \ m^{-1} \ s^{-2}\) |
Stress |
Pa |
pascal |
\(kg \ m^{-1} \ s^{-2}\) |
Energy |
J |
joule |
\(kg \ m^2 \ s^{-2}\) |
Work |
J |
joule |
\(kg \ m^2 \ s^{-2}\) |
Heat |
J |
joule |
\(kg \ m^2 \ s^{-2}\) |
Power |
W |
watt |
\(kg \ m^2 \ s^{-3}\) |
Electric Charge |
C |
coulomb |
\(A \ s\) |
Electric Potential (Voltage) |
V |
volt |
\(kg \ m^2 \ s^{-3} \ A^{-1}\) |
Electric Resistance |
\(\Omega\) |
ohm |
\(kg \ m^2 \ s^{-3} \ A^{-2}\) |
Magnetic Flux |
Wb |
weber |
\(kg^{-1} \ m \ s^{-2} \ A^{-1}\) |
Luminous Flux |
lm |
lumen |
\(cd \ sr\) |
USCS Derived Units#
The table below shows a number of derived units in the USCS or English/Imperial unit system.
Quantity |
USCS Units |
|---|---|
Acceleration |
\(ft \ s^{-2}\) |
Area |
\(ft^2\) |
Density |
\(slug \ ft^{-3}\) |
Energy |
\(Btu\) |
Force |
\(lb_f\) |
Velocity |
\(ft \ s^{-1}\) |
Volume |
\(ft^3\) |
SI Prefixes#
SI units are part of the metric system, which is convenient for engineering and scientific calculations because the units are categorized by factors of 10. The table below lists the metric prefixes and symbols used to denote various factors of 10 in SI units. For example, a centimeter is one-hundredth of a meter (in symbols, \(1 \ cm = 10^{-2} \ m\)) and a kilometer is a thousand meters (\(1 \ km = 10^3 \ m\)). Similarly, a megagram is a million grams (\(1 \ Mg = 10^6 \ g\)), a nanosecond is a billionth of a second (\(1 \ ns = 10^{-9} \ s\)), and a terameter is a trillion meters (\(1 \ Tm = 10^{12} \ m\)).
The table below contains SI prefixes ranging from \(10^{30}\) to \(10^{−30}\) that are currently recognized and used.
Prefix |
Symbol |
Meaning |
|---|---|---|
quetta- |
Q |
\(10^{30}\) |
ronna- |
R |
\(10^{27}\) |
yotta- |
Y |
\(10^{24}\) |
zetta- |
Z |
\(10^{21}\) |
exa- |
E |
\(10^{18}\) |
peta- |
P |
\(10^{15}\) |
tera- |
T |
\(10^{12}\) |
giga- |
G |
\(10^{9}\) |
mega- |
M |
\(10^{6}\) |
kilo- |
k |
\(10^{3}\) |
hecto- |
h |
\(10^{2}\) |
deka- |
da |
\(10^{1}\) |
deci- |
d |
\(10^{–1}\) |
centi- |
c |
\(10^{–2}\) |
milli- |
m |
\(10^{–3}\) |
micro- |
\(\mu\) |
\(10^{–6}\) |
nano- |
n |
\(10^{–9}\) |
pico- |
p |
\(10^{–12}\) |
femto- |
f |
\(10^{–15}\) |
atto- |
a |
\(10^{–18}\) |
zepto- |
z |
\(10^{–21}\) |
yocto- |
y |
\(10^{–24}\) |
ronto- |
r |
\(10^{-27}\) |
quecto- |
q |
\(10^{-30}\) |
A few things to keep in mind when using metric prefixes:
You cannot “double them up”
No space between the prefix and the unit
CAPITALIZATION matters
For example, if you have measurements in petameters (1 Pm = \(10^{15}\) m), it is not proper to talk about megagigameters, although \(10^6 \times 10^9 = 10^{15}\).
5 pm is \(5 \times 10^{-12}\) m (5 picometers) while 5 Pm is \(5 \times 10^{15}\) m (5 petameters). A huge difference of \(10^{27}\) m, but only different by the capitalization of one letter.
Section Summary#
This section introduced two common unit systems:
International System of Units (SI), also called the metric system
United States Customary System (USCS), also called the English or imperial system.
There are seven fundamental base quantities (length, mass, time, electric current, temperature, amount of substance, and luminous intensity). Derived units, which are combinations of base units, include examples such as area (\(m^2\)) and speed (\(m/s\)). Metric prefixes express large or small quantities in a manageable way and can be placed in front of SI units to modify their scale. Understanding these concepts is essential for effectively communicating and manipulating physical measurements in scientific and engineering contexts.
