5.5. Unit Vectors

A unit vector is a vector of unit length (magnitude of 1) used to specify a given direction.

The most common unit vectors are the Cartesian unit vectors \(\hat{i}\), \(\hat{j}\), and \(\hat{k}\).

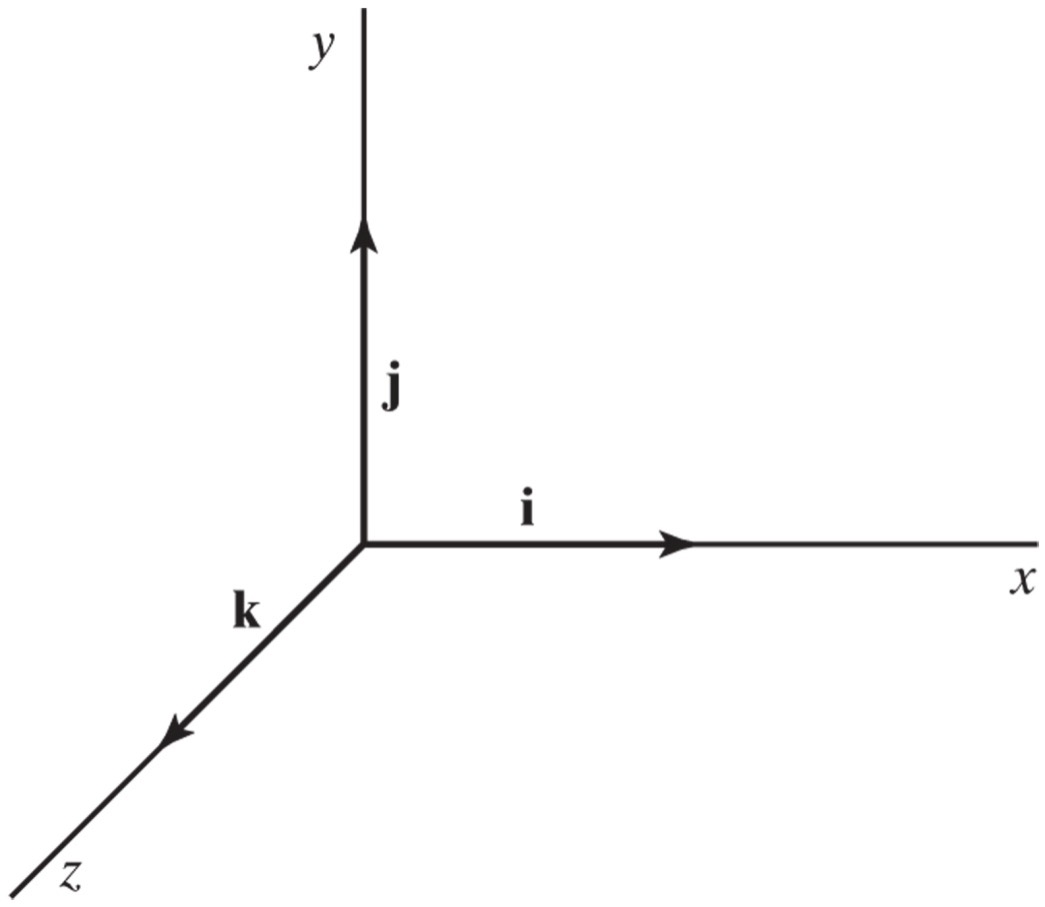
\[ \hat{i} = \langle1,0,0\rangle \]

\[ \hat{j} = \langle0,1,0\rangle \]

\[ \hat{k} = \langle0,0,1\rangle \]

In a 2-D Cartesian system, \(\vec{A}\) can be written in either matrix form

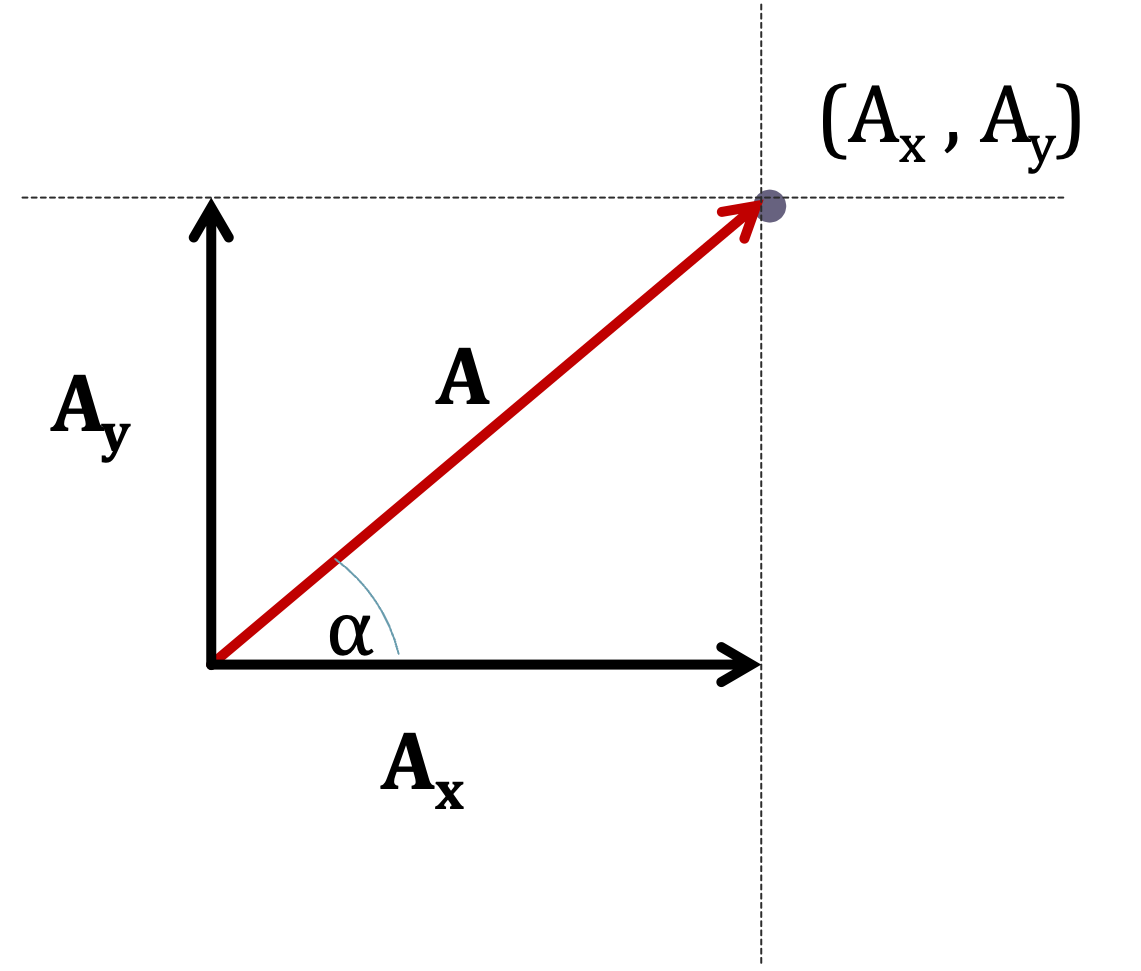
\[ \vec{A} = A\langle\cos\alpha,\sin\alpha\rangle \]

\[ \vec{A} = \langle A\cos\alpha,A\sin\alpha\rangle \]

Or unit vector notation form (also called \(\hat{i}\), \(\hat{j}\), \(\hat{k}\) notation), Where \(A\) is the magnitude of \(\vec{A}\)

\[ \vec{A} =A(\cos{\alpha}\hat{i} + \sin{\alpha}\hat{j}) \]

\[ \vec{A} =A\cos{\alpha}\hat{i} + A\sin{\alpha}\hat{j} \]

\[ \vec{A} =A_x\hat{i} + A_y\hat{j} \]